Mengetik merupakan pekerjaan yang tidak asing bagi seseorang yang bekerja di depan komputer dan sudah menjadi aktivitas wajib bagi seorang bloger atau penulis. Saat ini mungkin kita masih mengetik dengan dua jari dan itu  pun dibarengi dengan melihat keyboard. Mengetik dengan menggunakan dua jari atau 10 jari tidaklah menjadi masalah, namun apabila pekerjaan kita banyak dan menuntut untuk cepat, maka disarankan kita mampu mengetik dengan 10 jari.

Untuk kita mampu mengetik 10 jari bukan satu perkara yang instan, karenanya kita harus berlatih dan belajar mengetik 10 jari agar sebelum akhirnya kita terbiasa. Untuk belajar mengetik 10 jari kini tidak sulit, terdapat banyak cara untuk memelajarinya, misalnya aplikasi game, video  tutorial ataupun tutorial online lewat website, berikut ini 5 website sebagai media  belajar mengetik 10 jari.

Rapid Typing

Rapid Typing merpaukan aplikasi pembelajaran bagaimana mengetik cepat dan akurat, untuk menggunakan aplikasi ini kita dapat mendownloadnya langsung dari situs officialnya  rapydtyping.com  rapid typing zone menyediaan aplikasi tutorial, teknik pengetikan, game dan lainnya. pada halam situs rapid typing kita pun dapat melakukan belajar langsung dngan test secara online.

Test Online rapid typing

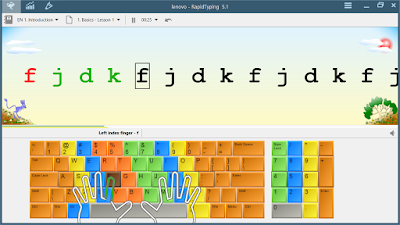aplikasi tutorial rapid typing

www.typingstudy.com

Pada situs ini kita bisa belajar langsung secara onlie bagaimna cara mengetik cepat dan efektif, pembelajaran dapat dilakukan dengan mengikuti turial teks yag dibantu dengan gambar tutorial yang mudah untuk dipahami.

typing study

10fastfingers.com 

 Untuk menggunanakan website ini kita tidak usah bingung, karena website ini dibuat dengan tampilan untuk memudahhkan setiap pengguna baru.

Pada halaman utuama situs kita langsung menginputkan teks pada kolom input, kita diberi waktu 1 menit sebagia waktu standar pengetika  dan apabila waktu habis maka akan keluar skor berapa cepat kita mengetik dan seberap aurat kita mengetik.

 10fastfingers.com 

Typeracer.com

Sesuai dengan namanya typeracer pada situs ini  memungkinkan kita untuk bermain game dengan berlomba satu sama lain.engetikkan  dengan kutipan dari buku , film , dan lagu dan sebagainya . Typeracer diluncurkan pada tahun 2010 , bertujuan untuk menjadi produk pendidikan yang paling menyenangkan di dunia . Dirancang untuk K - 12 sekolah , itu memanfaatkan konsep permainan TypeRacer yang ternyata mengetik menjadi olahraga dan membuat belajar menyenangkan

Typeracer

Ngetik.web.id

Hampir sama dengan beberapa situs web sebelumnya, pada website ngetik.web.id kita dapat menguji tes kemampuan mengetik kita. untuk dapat menggunakan situs ini tentu sangatlah mudah,. Menggunakan tampilan yang sederhana situs ini membuat kita lebih mudah untuk menggunakannya.

ngetik.web.id

Konversi Bentuk Standar dan Kanonik

Dengan hukum de morgan :
F = (m0 + m2 + m3)    = m0’ .m2’.m3’
                                    = M0M2M3
                                    = ∏ (0,2,3)
jadi,     mj’                   = Mj
sehinga :          F(x,y,z) = ∏ (0,2,4,5)
dikonversikan ke SOP, menjadi :
            F(x,y,z)             = Σ(1,3,6,7)

Contoh Kasus:

1.      Cari bentuk standar dari f(x,y)           = x’

Jawab :
f (x,y)   = x’.(y+y’)
            = x’y+x’y’         bentuk standar SOP
            = m0+m1
dengan mj’ = Mj

maka :
f’(x,y)               = xy’+xy
(f’(x,y))’           = (x+y’) (x+y)   {bentuk standar SOP}
                        = M2M3

2.      Cari bentuk standar dari f(x,y,z) = y’ + xy +x’yz’

Jawab :

f(x,y,z)                         = y’+ xy + x’yz’ {lengkapi literal pada setiap suku}
                        = y’(x + x’)(z + z’) + xy(z + z’)x’yz’
                        = (xy’ + x’y’)(z + z’) + xyz + zyx’ + x’yz’
                        = xy’z + xy’z’ + x’y’z + x’y’z’ + xyz + xyz’+ x’yz’
                        = m0 + m1 + m2 + m4 + m5 + m6 + m7

atau f(x,y,z)     = x + t’ +z’
= M3

3.      Cari bentuk kanonik ;

a)      f(x,y)          = x’y + xy’

tabel nilainya        :

X   Y	Minterm			Maxterm
	Term	Des	Value	Term	Des	Value
0    0 0        1 1        0 1    1	xy’ x’y xy’ xy	m0 m1 m2 m3	0 1 1 0	x+y x+y’ x’+y x’+y’	M0 M1 M2 M3	0 1 1 0

Dari tabel :

Nilai 1: minterm : f(x,y)    = m1 + m2       = Σ(1,2)
nilai 0 : maxteerm : f(x,y) = M0.M3m      = ∏(0,3)

Cara konversi :

F’(x,y)        = x’y’+xy          = m0 + m3  {dari tabel}

Dual-nya

f’(x,y)         = (x’+y’).(x+y)

f(x,y)          = (x+y).(x’+y’) = M0.M3

b)      F (0x,y,z)    = F = x’y’z + xy’z’+ xyz

Tabel nilai (ringkas) :

X	Y	Z	Minterm	Maxterm	F
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	x’y’z’ x’y’z x’yz’ x’yz xy’z’ xy’z xyz’ xyz	x+y+z x+y+z’ x+y’+z x+y’+z’ x’+y+z x’+y+z x’+y’+z x’+y’+z’	0 1 0 1 0 1 0 1

Jadi f(x,y,z) = m1+m4+m7 = Σ(1,4,7)

                  = M0.M2.M3.M5.M6 = ∏ (0,2,3,5,6)

Cara konversi :

Dari tabel diperoleh :

F’(x,y,z)      = x’y’z’ + x’yz’ + x’yz + xy’z + xyz’

Dual :

F = (x’+y’+z’) (x’+y+z’) (x’+y+z) (x+y’+z) (x+y+z’)

Seingga

f(x,y,z)       = (x+y+z) (x+y’+z) (x+y’+z’) (x’+y+z’) (x’+y’+z)

                 = M0.M2.M3.M5.M6

Konversi Ke bentuk Sum Of Product (SOP)

Cara konversi entuk SOP (Sum Of Product) adalah sebagai berikut:

Nyatakn fungsi boolean f= A+B’C dalam SOP

Jawab :

a)      Harus dilengkapi dahulu literal untuk tiap suku agar sama

-          Suku ke – 1            A   = A(B+B’)
                                     = AB + AB’

Lengka[i literal untuk tiap suku
suku ke -1-1 :         AB = AB(C+C’)
                                     =  ABC+ABC’

suku ke -1-2 :         AB = AB’(C+C’)

                                     = AB’C+AB’C’

Sehingga suku ke-1 menjadi :

ABC + ABC’ +AB’C+AB’C’

Suku ke -2              B’C = B’C(A+A’)

                                     = AB’C + A’B’C

b)      Jumlah suku dengan literal  yang lengka[ , sehingga

F= ABC+ ABC’+ AB’C+ AB’C’+ AB’C+ A’B’C

c)      Sederhanakanlah agar tidak ada suku yang sama, sehingga :

 F= ABC+ ABC’+ AB’C+ AB’C’+ A’B’C

(notasi ini adalah ) notasi umum untuk menyatakan bentuk kanonik untuk fungsi boolean)

Konversi ke bentuk Produk Of Sum (POS)

Cara konversi ke bentuk Produk Of Sum (POS) adalah sebagai berikut :
nyatakan fungsi boolean F = xy + xz’ dalam POS

Jawab :

a)      Bentuk fungsi dalam POS

F    = xy+x’z

      = (xy + x’) ( xy+z)  {distributif}
      = (x+x’) (y+x’)(x+z)(y+z)

      = (x’+y)(x+z)(y+z)

b)      Lengkapi literal tiap suku :

Suku ke 1   x’+ y     = x’+y + zz’

                              = (x’y+ z) (x’+y+z’)

Suku ke 2   x + y     = x + z + yy’

                              = (x + y + z) (x + y’+ z)

Suku ke 3   y +z      = y + z + xx’

                              = (x + y + z) (x’ + y + z)

c)      Jumlah suku untuk semua suku dengan literalyang lengkap :

F = (x + y + z) (x + y’ + z) (x’ + y + z) (x’ + y + z’)

   = M0.M2.M4.M5

Atau dengan notasi lain = ∏ (0,2,5,6)

(bentuk kanonik POS)

               

DEFINISI

Misalkan x₁,x₂.......x_n  merupakan variabel-variabel aljabar Boolean. Boolean dengan n variabel adalah fungsi yang dapat dibentuk dari aturan-aturan berikut :

1.       Fungsi konstan :
f(x₁,x₂,x₃,x₄......x) =

2.       Fungsi proyeksi

F(x₁,x₂,x₃,....x_n) =x   I= 1,2,... n

3.       Fungsi komplemen

g(x₁,x₂,x₃,....x_n)  = (f(x₁,x₂,x₃,....x_n))

fungsi gabungan

h(x₁,x₂,x₃,....x_n) = f(x₁,x₂,x₃,....x_n)+g(x₁,x₂,x₃,....x_n)

h(x₁,x₂,x₃,....x_n) = f(x₁,x₂,x₃,....x_n)●g(x₁,x₂,x₃,....x_n)

catatan :

fungsi identitas ; fungsi proyeksi satu variabel, dimana f(x)=x

contoh

berikuat adalah fungsi-fungsi boolean dengan variabel x,y, dan z dan a yang merupakan elemen dalam aljabar:

f(x)                 = x + x’a
g(x,y)            = x’y+xy’+y

h(x,y,z)         = axy’z=yz’+a+xy

Teorema

jika f adalah Boolean dengan satu variabel maka untuk semua nilai x adalah

f(x) = f(1)x+f(0)x’
untuk kemungkinan bentuk f :

kasus 1 :

f adalah fungsi konstan , f(x) = a
f(1)x+f(0)x’ = ax+ax’ = a(x+x’) = a1 = f(x)

kasus 2:

f adalah fungsi identitas
f(1)x+f(0)x’ = 1’+0x’ = x+0 = x = f(x)

kasus 3

h(x) = f(x)+g(x)

h()x = f(x)+g(x) = f(1)x+f(0)x’+g(1)x+g(0)x
                                                = (f(1)+g(1))x+(f(0)+ g(0))
                                                = h(1)x+h(0)x’

kasus 4

k()x        = f(x)g(x)
k()x        = f(x)g(x) = (f(1)x+f(0)x’)(g(1)x+g(0)x’)
                = f(1)g(1)xx+f(1)g(0)xx’+f(0)g(1)x’x+f(0)g(0)x’x’
                = f(1)g(1)x+f(0)g(0)x’
                = k(1)x+k(0)x’

bentuk diatas adalah bentuk kanonik fungsi boolean satu variabel, dengan cara yang sama jika f adalah fungsi boolena dengan dua variabel, maka untuk nilai x dan y bentuk kanoniknya adalah sebagai berikut :

f(x,y) = f(1,1)xy + f(1,0)xy’+f(0,1)x’y+ f(0,0)x’y’

Rumus Umum Bentuk Kanonik

Rumus pembentukan bentuk kanonik f fungsi boolean dengan n variabel adalah sebagai berikut:
f(x₁.....x_n)= f(e₁......e₂)x₁^e ₁x₂^e₂.....x_n ^e_n

Dimana e₁ bernilai 0 dan  x₁^e ₁ diartikan sebagai x₁  atau x₁^e’ sesuai dengan e₁ (bernilai 1 atau 0)

BENTUK FUNGSI

Suatu fungsi dapat dinyatakan dalam berbagai bentuk berbeda tapi mempunyai arti yang sama.

Contoh fungsi – fungsi boolean berikut :

f(x)         = x+ x’a

g(x,y)    = x’y +xy’+y’

h(x,y)    = x’y’

k(x,y)    = (x+y)’

f1(x,y)   = x’.y’

f2(x,y)   = (x+y)

dengan menggunakan hukum de morgan dapat dinyatakan bawa h dan k adalah fungdi yang sama, juga untuk fungsi f1 dan f2. Dapat disimpulkan bahwa berapa fungsi boolean mungkin mempunyai bentuk berbeda tetapi nilainnnya sama. Olelh karena itu, diperlukan cara untuk menentukan apakah dua ekspresi boolean ynag mempresentasikan mempunyai nilai sama. Cara tersebut adalah menggunakan bentuk standar atau bentuk kanonik.

Contoh

Fungsi boolean

F(x) = x+x’a

Dimana f mempunyai elemen aljabar boolean yaitu 0,a,a’, 1.  tentukan bentuk kanoniknya  !

Maka kita harus melakukan pemeriksaan untuk semua elemen fungsi, yaitu :

X	f(x)
0 a a’ 1	0 + 1.a = a a + a’.a =a = 0 + a a’=a.aa = a’ +a =1 1 + 0.1 = 1 + 0 = 1

 Kita dapat memperoleh bentuk kanoniknya sebagai berikut :

f(x)         = f(1)x+f (0)x’
                =1.x + a.x’
                = x+ax’
                = (x+a).(x+x’)
                = (x+a).1
                = x+a

kegunakan bentuk kanonik

bentuk kanonik digunakan untuk menentukan apakah dua ekspresi merupakan fungsi yang sama.

Seringkali fungsi Boolean dinyatakan dengan operasi yang berlebihan. Kita dapat mengkorversi bentuk fungsi Boolean menjadi bentuk minimum, yaitu fungsi yang masih menghasilkan nilai sama tapi dengan jumlah operasi yang minimum,

Cara representasi fungsi Boolean dapat dinyatakan secara :

1.       Aljabar

2.       Dengan tabel kebenaran

Contoh : Fungsi F = xyz’

Refresentasi  secara aljabar adalah F = xyz’

Refresentasi dengan tabel kebenarannya adalah sebagai berikut

X   Y   Z	F
0   0   0 0   0   1 0   1   0 0   1   1 1   0   0 1   0   1 1   1   0 1   1   1	0 0 0 0 0 0 1 0

Jumlah elemen dalam tabel kebenaran adalah jumlah kombinasi dari nilai variabel-variabelnya, yaitu sejumlah 2ⁿ dimana n adalah banyaknya variabel biner.

Konversi dari tabel kebenaran

Fungsi boolean yang diinyatakan tabel kebenaran dapat dikorversi menjadi bentuk aljabar.

Contoh fungsi boolean dengan tabel kebeanran sebagai berikut :

X   Y   Z	F
0   0   0 0   0   1 0   1   0 0   1   1 1   0   0 1   0   1 1   1   0 1   1   1	0 1 0 0 1 0 0 1

Dari tabel kebenaran:

(1)    F₁                  = x’y’z +xy’z’ +xyz

= m11 +m4 +m7

F1           = x’y’z’ + x’yz’ +x’yz + xy’z + xyz’

Atau

(2)    F1           = (x+y+z)(x+y’+z)(x+y’+z’)(x’+y+z’)(x’+y’+z)

= (F1’)’
= M0 M2 M3 M5 M6

Bentuk (1) dan (2) merupakan fungsi/bentuk standar, yaitu fugsi yang literalnya ditulis lengkap pada tiap suku

1.       Bentuk pertama (1) disebut SOP (Sum Of Product)/ Mintrem

2.       Bentuk kedua (2) disebut POS (Product of Sum)/ Maxtrem

Fungso Boolean yang diekspresikan dalam bentuk SOP atau POS disebut fungsi/bentuk Kanonik.

BENTUK STANDAR DAN BENTUK KANONIK

Bentuk Standar Dan Bentuk Kanonik 2 Variabel

x y	Sum Of Product (SOP)		Product Of Sum (POS)
	Term	Nilai	Term	nilai
1 1 1 0 0 1 0 0	xy xy’ x’y’ x’y	M3 M2 M1 M0	X’ + y’ X’ + y X  + y X  + y	M3 M2 M1 M0

Bentuk Standar Dan Bentuk Kanonik 3 Variabel

x y	Sum Of Product (SOP)		Product Of Sum (POS)
	Term	Nilai	Term	nilai
1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0	xyz xyz’ xy’z xy’z’ x’yz x’yz’ x’y’z x’y’z’	m7 m6 m5 m4 m3 m2 m1 m0	x’ + y’+z’ x’ + y’ +z x‘ + y +z’ x’ + y +z x  + y’ +z’ x  + y’ +z x  + y +z’ x  + y +z	m7 m6 m5 m4 m3 m2 m1 m0

Sumber : Logika Matematika ( Retno Hendrowati, Ir.,MT)